Chapter 9 Hedonic rating (e.g. liking scores)
An evaluation of how much we like a food or drink is a hedonic response. Often this is given as a number on a scale, or by checking a category box with a description, such as the 9-point hedonic scale. For data analysis, the boxes are made numerical, with the assumption the there is equidistance between the meaning of the category labels, i.e dislike extremely and dislike very much is as different as dislike a little and neutral. The original English language anchors for the 9-point hedonic scale was develop and validated on tests using approximately 5500 American soldiers in the beginning of the 1950’s (Lawless & Heymann, Chapter 7 Scaling, 2010). There are a number of validated scales, including visual smiley scales for children. Dependent on the respondent 5, 7 or 9 point scales are used.
Most often we want to know if the hedonic response is significantly different (not just different by chance) depending on the samples. We might also want to know if other factors have an influence on the hedonic rating. e.g. household income or sex. We also want to know what are the actual differences are in numerical size. All this requires different statistical estimates.
9.1 Plotting liking scores
For the beer data we have the liking in a long matrix.
library(data4consumerscience)
library(ggplot2)
data(beerliking)A histogram of the likings shows that some are symmetric ( NY Lager, River Beer and to some extend Porse Bock), while Brown Ale and Ravnsborg Red is skeew, and Wheat IPA is uniform.
ggplot(data = beerliking, aes(Liking)) +
geom_histogram() +
facet_wrap(~Beer)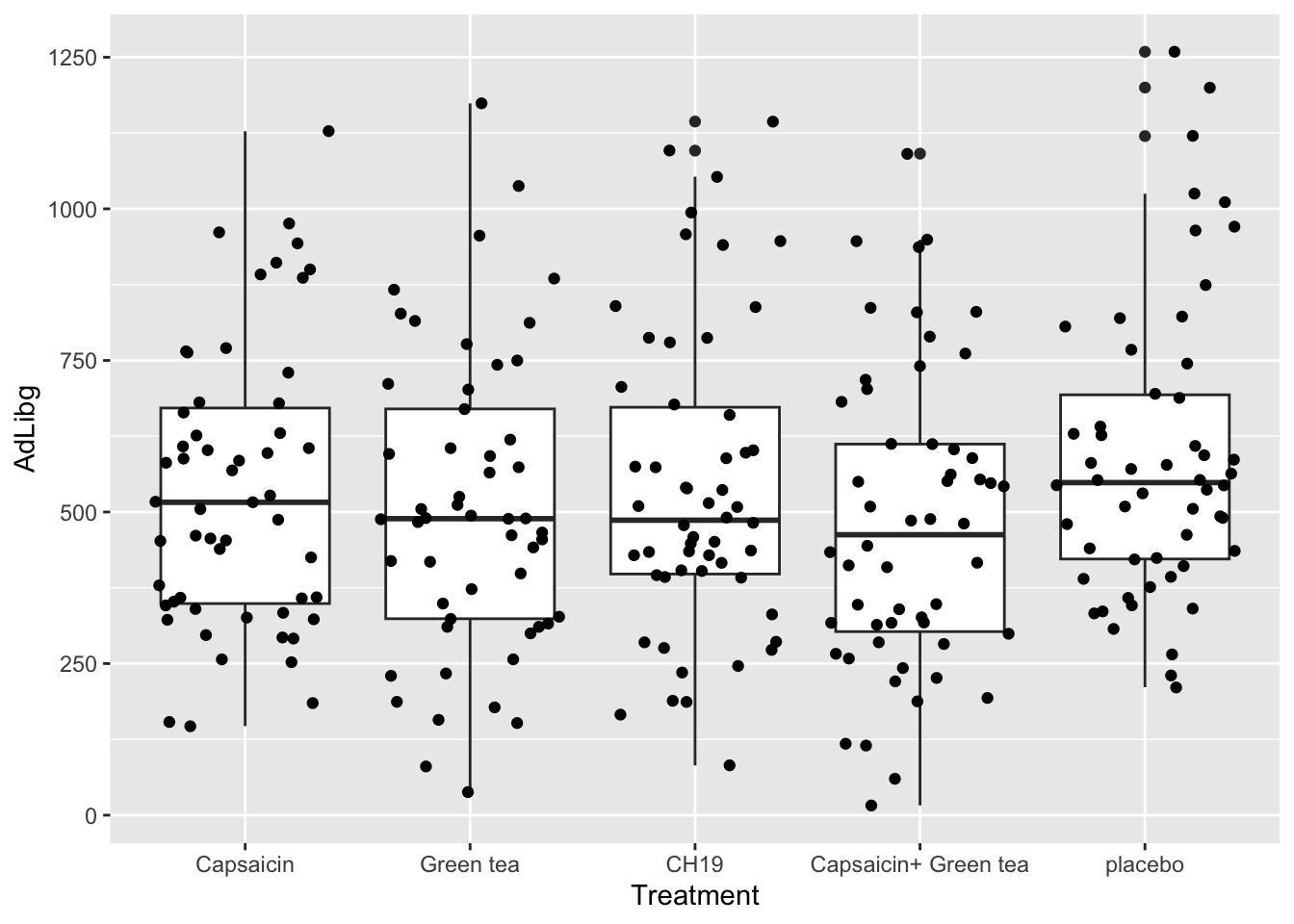
9.2 Simple mixed models
In the following plot each liking score is connected within consumer across the beer types. The facet (according to Age) is just to avoid overplotting.
Here, there is a trend towards, if you rate one beer high, the other likings within that consumer will also be high.
ggplot(data = beerliking, aes(Beer,Liking, group = Consumer.ID, color = Consumer.ID)) +
geom_point() +
geom_line() +
theme(legend.position = 'none') +
facet_wrap(~Age)
Mixed models are used when there is repetitions in the response due to (here) the person tasting more than one product.
library(lmerTest)
library(lme4)
mdl <- lmer(data = beerliking, Liking ~ Beer + (1|Consumer.ID))
summary(mdl)## Linear mixed model fit by REML. t-tests use Satterthwaite's method [
## lmerModLmerTest]
## Formula: Liking ~ Beer + (1 | Consumer.ID)
## Data: beerliking
##
## REML criterion at convergence: 3602.4
##
## Scaled residuals:
## Min 1Q Median 3Q Max
## -2.52447 -0.73529 0.08622 0.74232 2.01132
##
## Random effects:
## Groups Name Variance Std.Dev.
## Consumer.ID (Intercept) 0.3242 0.5694
## Residual 2.6615 1.6314
## Number of obs: 920, groups: Consumer.ID, 155
##
## Fixed effects:
## Estimate Std. Error df t value Pr(>|t|)
## (Intercept) 4.9017 0.1401 866.2019 34.985 < 2e-16 ***
## BeerNY Lager -0.6413 0.1869 763.6045 -3.431 0.000634 ***
## BeerPorse Bock -0.8369 0.1866 762.9501 -4.485 8.40e-06 ***
## BeerRavnsborg Red -0.2330 0.1866 762.9501 -1.249 0.212179
## BeerRiver Beer -0.8367 0.1866 764.6334 -4.483 8.47e-06 ***
## BeerWheat IPA -0.9419 0.1869 763.6045 -5.040 5.83e-07 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Correlation of Fixed Effects:
## (Intr) BrNYLg BrPrsB BrRvnR BrRvrB
## BeerNYLager -0.669
## BeerPorsBck -0.670 0.503
## BrRvnsbrgRd -0.670 0.503 0.504
## BeerRiverBr -0.671 0.502 0.503 0.503
## BeerWhetIPA -0.669 0.502 0.503 0.503 0.502Here we see that the residual uncertainty is \(1.63\) on the 1-7 likert scale, while the uncertainty between consumers is \(0.57\). This implies that the uncertainty between two ratings is higher when from two different consumers, compared to two ratings from the same consumer.
We can use this model to evaluate the effect of the different beers.
anova(mdl)## Type III Analysis of Variance Table with Satterthwaite's method
## Sum Sq Mean Sq NumDF DenDF F value Pr(>F)
## Beer 110.52 22.105 5 763.12 8.3054 1.175e-07 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1It seems as the average liking is different between beers.
9.2.1 Post hoc test
The overall anova result implies that the 6 beers are NOT equal in terms of liking, but some may be similar.
This can be investigated by computing pairwise contrasts using for instance the emmeans package or the multcomp package.
Both are shown below
library(emmeans)
mdlemm <- emmeans(mdl,'Beer')
contrast(mdlemm,'tukey')## contrast estimate SE df t.ratio p.value
## Brown Ale - NY Lager 0.641267 0.187 762 3.431 0.0083
## Brown Ale - Porse Bock 0.836859 0.187 762 4.485 0.0001
## Brown Ale - Ravnsborg Red 0.232963 0.187 762 1.249 0.8126
## Brown Ale - River Beer 0.836742 0.187 763 4.483 0.0001
## Brown Ale - Wheat IPA 0.941921 0.187 762 5.040 <.0001
## NY Lager - Porse Bock 0.195592 0.186 761 1.050 0.9006
## NY Lager - Ravnsborg Red -0.408304 0.186 761 -2.192 0.2425
## NY Lager - River Beer 0.195475 0.186 763 1.049 0.9010
## NY Lager - Wheat IPA 0.300654 0.187 761 1.612 0.5909
## Porse Bock - Ravnsborg Red -0.603896 0.186 761 -3.248 0.0153
## Porse Bock - River Beer -0.000117 0.186 762 -0.001 1.0000
## Porse Bock - Wheat IPA 0.105061 0.186 761 0.564 0.9933
## Ravnsborg Red - River Beer 0.603779 0.186 762 3.247 0.0154
## Ravnsborg Red - Wheat IPA 0.708957 0.186 761 3.807 0.0021
## River Beer - Wheat IPA 0.105178 0.186 763 0.565 0.9932
##
## Degrees-of-freedom method: kenward-roger
## P value adjustment: tukey method for comparing a family of 6 estimatesTo calculate pairwise comparisons between e.g. samples and find letter-based representation you need a the package multcomp.
library(multcomp)
cld(glht(mdl, linfct = mcp(Beer = "Tukey")))## Brown Ale NY Lager Porse Bock Ravnsborg Red River Beer
## "c" "ab" "a" "bc" "a"
## Wheat IPA
## "a"The letters are based on the Post Hoc test Tukey, and they are calculated on the basis of the model mdl. Samples with the same letters are not significantly different. You can only use this function on factors.
The resulst indicate Brown Ale and Ravnsborg Red is the most likable beers, with River Beer, Wheat IPA and Porse Bock as the least likable ones. These three at the bottom is also not significantly different.
9.3 Multivariable models
In the example above, only the impact of the different beers is evaluated, however, the liking scores may also depend on background information such as gender, age, … as well as attitude towards beer and food. Further, is there any of the background variables that attenuate or make the differences between the beers stronger? These questions can be investigated by models including several explanatory variables as well as interaction terms.
9.3.1 Additive models
This can be included in the models as a sequence of explanatory variables.
Given a set of possible explanatory variables, there is two ways to include them in the model.
Forward step-wise Selection and Backward Step-wise Elimination.
For both, the principle is simple and intuitive.
In the forward procedure each variable is added to the model, and the strongest one (in terms of the lowest p-value) is kept.
In the backward procedure all variables are added to the model and the least important one (in terms of the largest p-value) is removed.
Both procedures stop when the model is not going to improve by adding or eliminating explanatory variables, and the final model will only contain the significant variables.
In the beer dataset we would like to know which of the explanatory variables that is most related to the liking.
A large model with all explanatory variables is constructed
mdl_be <- lmer(data = beerliking, Liking ~ Beer + Gender + Age + Income +
Householdsize + `Beer types/month` + `Interest in food` +
neophilia + `Interest in beer` + `Beer knowledge` +
`Ingredients/labels` + `Future interest in beer` +
(1|Consumer.ID))
anova(mdl_be)## Type III Analysis of Variance Table with Satterthwaite's method
## Sum Sq Mean Sq NumDF DenDF F value Pr(>F)
## Beer 110.799 22.1597 5 762.75 8.3223 1.133e-07 ***
## Gender 0.093 0.0932 1 125.57 0.0350 0.851886
## Age 20.946 3.4911 6 129.73 1.3111 0.256695
## Income 47.126 7.8544 6 126.31 2.9498 0.009962 **
## Householdsize 7.385 1.2309 6 127.84 0.4623 0.835121
## `Beer types/month` 17.519 4.3797 4 125.10 1.6448 0.167136
## `Interest in food` 0.015 0.0149 1 127.62 0.0056 0.940561
## neophilia 2.730 2.7305 1 125.27 1.0255 0.313179
## `Interest in beer` 1.092 1.0923 1 125.69 0.4102 0.523029
## `Beer knowledge` 1.019 1.0186 1 127.44 0.3825 0.537350
## `Ingredients/labels` 1.742 1.7424 1 130.36 0.6544 0.420024
## `Future interest in beer` 8.480 8.4798 1 128.45 3.1847 0.076692 .
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1From this, Interest in food is the least significant one, and is hence removed.
A sequential removal of the non-significant variables at a \(p > 0.1\) level leads to the following model:
mdl_be_red <- lmer(data = beerliking, Liking ~ Beer + Age + Income +
`Beer types/month` + `Beer knowledge` +
`Future interest in beer` +
(1|Consumer.ID))
anova(mdl_be_red)## Type III Analysis of Variance Table with Satterthwaite's method
## Sum Sq Mean Sq NumDF DenDF F value Pr(>F)
## Beer 110.397 22.079 5 763.19 8.2936 1.206e-07 ***
## Age 31.657 5.276 6 140.10 1.9819 0.0721622 .
## Income 53.130 8.855 6 136.92 3.3261 0.0043400 **
## `Beer types/month` 22.526 5.631 4 135.80 2.1153 0.0822411 .
## `Beer knowledge` 7.624 7.624 1 136.44 2.8638 0.0928735 .
## `Future interest in beer` 32.101 32.101 1 136.94 12.0579 0.0006906 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1The results can be interpreted from the estimates:
summary(mdl_be_red)## Linear mixed model fit by REML. t-tests use Satterthwaite's method [
## lmerModLmerTest]
## Formula:
## Liking ~ Beer + Age + Income + `Beer types/month` + `Beer knowledge` +
## `Future interest in beer` + (1 | Consumer.ID)
## Data: beerliking
##
## REML criterion at convergence: 3565.3
##
## Scaled residuals:
## Min 1Q Median 3Q Max
## -2.6308 -0.7514 0.1098 0.7695 2.3071
##
## Random effects:
## Groups Name Variance Std.Dev.
## Consumer.ID (Intercept) 0.1282 0.358
## Residual 2.6622 1.632
## Number of obs: 920, groups: Consumer.ID, 155
##
## Fixed effects:
## Estimate Std. Error df t value Pr(>|t|)
## (Intercept) 3.90704 0.27947 204.93561 13.980 < 2e-16 ***
## BeerNY Lager -0.64282 0.18691 763.70251 -3.439 0.000615 ***
## BeerPorse Bock -0.83812 0.18659 763.00699 -4.492 8.15e-06 ***
## BeerRavnsborg Red -0.23422 0.18659 763.00699 -1.255 0.209758
## BeerRiver Beer -0.83263 0.18666 764.83113 -4.461 9.39e-06 ***
## BeerWheat IPA -0.94359 0.18691 763.79940 -5.048 5.57e-07 ***
## Age26 - 35 0.69239 0.23903 137.28362 2.897 0.004390 **
## Age36 - 45 0.67901 0.27355 135.35332 2.482 0.014279 *
## Age46 - 55 0.67519 0.23620 136.98329 2.859 0.004922 **
## Age56 - 65 0.56954 0.22746 135.55073 2.504 0.013468 *
## Age66 - 75 0.42221 0.26112 135.16072 1.617 0.108222
## AgeOver 75 0.35509 0.54746 157.45623 0.649 0.517532
## Income10.000 - 20.000 -0.61069 0.20865 136.06552 -2.927 0.004015 **
## Income20.000 - 30.000 -0.95496 0.26153 136.81905 -3.651 0.000370 ***
## Income30.000 - 40.000 -0.96093 0.28842 136.58309 -3.332 0.001111 **
## Income40.000 - 50.000 -0.77668 0.26949 136.19196 -2.882 0.004592 **
## Income50.000 - 60.000 -0.91177 0.25817 135.14344 -3.532 0.000565 ***
## IncomeOver 60.000 -0.52614 0.26889 136.07315 -1.957 0.052427 .
## `Beer types/month`3 - 4 -0.13295 0.15506 135.94213 -0.857 0.392732
## `Beer types/month`5 - 8 0.27227 0.20909 136.15421 1.302 0.195044
## `Beer types/month`9 - 16 0.42102 0.49514 135.41930 0.850 0.396657
## `Beer types/month`Over 16 0.97824 0.58046 135.69832 1.685 0.094229 .
## `Beer knowledge` 0.08520 0.05034 136.44151 1.692 0.092873 .
## `Future interest in beer` 0.16456 0.04739 136.93585 3.472 0.000691 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Some notes: Liking is higher in the lowest Income group, Liking is lower in the lowest age group, and liking is higher with higher Future interest in beer.
9.3.2 Effect modification and Interactions
It could be nice to calculate if the liking of specific sample are affected by the degree of future interest in beer. This can be visualized as scatterplots and modelled using interactions.
ggplot(data = beerliking, aes(`Future interest in beer`, Liking, color = Beer)) +
geom_point() + stat_smooth(se = F, method = lm)
mdl_interaction <- lmer(data = beerliking, Liking ~ Beer*`Future interest in beer` + (1|Consumer.ID))
anova(mdl_interaction)## Type III Analysis of Variance Table with Satterthwaite's method
## Sum Sq Mean Sq NumDF DenDF F value Pr(>F)
## Beer 14.431 2.886 5 758.29 1.0898 0.3645
## `Future interest in beer` 65.599 65.599 1 153.35 24.7694 1.718e-06
## Beer:`Future interest in beer` 23.230 4.646 5 758.06 1.7543 0.1200
##
## Beer
## `Future interest in beer` ***
## Beer:`Future interest in beer`
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Although the slopes appear a bit different between the beers this is not significant (\(p = 0.12\)). Be aware that it appears as the main effect of beer is not significant. However, this value should not be interpreted, as there are interaction terms in the model including beer.
Remember you choose your own “name” for the model “+” between variables defines (additive) main effects “:” between variables defines an interaction “*” between variables defines a parameterization with both interaction and main effect terms
For model selection here, you start by removing the interaction with the hight p-value and then recalculate the model. You cannot remove a single variable if an interaction including it is significant.