Chapter 4 Descriptive statistics

In this Chapter we will go through the main elements of descriptive statistics.

In principle, descriptive statistics is the act of taking a bunch of data and represent them in few numbers, such as mean, median, standard deviation etc.

For a more thorough introduction you can check every introductory stats book: The first couple of chapters will cover this.

For examples in this chapter we will use two datasets: chili: where and green tea in combination is added to meals and the resulting ad-libitum consumption is recorded, and pasta which is iBuffet data with a survey of preferences for each Person.

library(data4consumerscience)
data(chili)
data(pasta)
# we subset to only have the "Pasta with legumes" data. 
pasta <- pasta[pasta$StationName=='Pasta with legumes',]

If you do not have imported the data4consumerscience package see: Import data from R-package If you need to import data see: How to import data

4.1 Descriptives for a continuous variable

Below we will first explain the different descriptive measures, and then describe calculations of them. Continuous variables could be sensory scores (e.g. 15 cm continuous line scale), consumption data (in gram) or liking scores (e.g. on a scale from 1 to 9).

4.1.1 Mean / median

Here you get an introduction to statistics, descriptive statistics and the terms average/mean and median:

4.1.2 Variance

Here you get an introduction to variance:

4.1.3 Standard deviation

Here you get an introduction to the standard deviation:

4.1.4 Calculations

For the calculations, we use the chili dataset. To compute mean, median, variance, standard deviation, etc. there are functions working directly on vectors/columns in you data frame. An easy way to specify this in R is using the $-sign after the name of your data frame, followed by the column name (e.g. chili$Totalg). na.rm = TRUE removes NA values in the vector. This can be done for all the below functions.

mean(chili$Totalg, na.rm = TRUE)

## [1] 1699.977

median(chili$Totalg)

## [1] 1740.4

var(chili$Totalg)

## [1] 211259

sd(chili$Totalg)

## [1] 459.6292

IQR(chili$Totalg)

## [1] 660.6

summary(chili$Totalg)

##    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
##   849.6  1289.1  1740.4  1700.0  1949.7  2905.2

4.2 Distributions of count data

If the response can take certain values or categories, then the table function is good in getting how many observations there are within a given vector, or combinations of several vectors.

table(pasta$I_like_taste_of_pasta_with_legumes)

## 
##  2  3  4  5  6  7 
##  1  3  2  5  8 11

table(pasta$I_like_taste_of_pasta_with_legumes, pasta$Did_you_consider_the_proteincontent_of_the_dishes_you_choose)

##    
##     No Yes
##   2  0   1
##   3  2   1
##   4  1   1
##   5  1   4
##   6  0   8
##   7  5   6

You see that most of the answers are in agreement with question, and that there are no observations in the Strongly disagree category.

This is a very high level representation, and we usually want to compare means (or other metrics) between different groups. That is to compute descriptive statistics for subsets of the data. There are two ways to do this. Either using the aggregate() function or use the group_by() and summarize() from the tidyverse framework.

Below both is shown to characterize Totalg on each of the products

4.3 Aggregate

aggregate(chili$Totalg,by = list(chili$Treatment),FUN = mean)

##                Group.1        x
## 1            Capsaicin 1716.195
## 2            Green tea 1664.504
## 3                 CH19 1708.977
## 4 Capsaicin+ Green tea 1649.495
## 5              placebo 1759.754

aggregate(chili$Totalg,by = list(chili$Treatment),FUN = sd)

##                Group.1        x
## 1            Capsaicin 473.1042
## 2            Green tea 462.2564
## 3                 CH19 452.1225
## 4 Capsaicin+ Green tea 450.3940
## 5              placebo 468.4211

aggregate() will apply a function to a column or data set, using the list provided to group the column or dataset.

In our case, the column we want to apply our function to is chili$Totalg, the functions are FUN = mean or FUN = sd (finding the mean and standard deviation, respectively) and the column we use for grouping the data is chili$Treatment.

This results in a data frame, where one column shows each unique group in chili$Treatment, and another column shows the mean or standard deviation of chili$Totalg corresponding to each group.

4.4 Tidyverse

… or you can do it using tidyverse:

library(tidyverse)
tb <- chili %>% 
  group_by(Treatment) %>% # specify which grouping vector to use
  dplyr::summarise(n = n(), # compute n
            mn = mean(Totalg), # compute mean
            s = sd(Totalg), # compute s
            q1 = quantile(Totalg,0.25), # compute lower 25% quartile
            q3 = quantile(Totalg,0.75)) # compute upper 75% quartile
tb  

## # A tibble: 5 × 6
##   Treatment                n    mn     s    q1    q3
##   <fct>                <int> <dbl> <dbl> <dbl> <dbl>
## 1 Capsaicin               55 1716.  473. 1314. 1943.
## 2 Green tea               53 1665.  462. 1213. 1912.
## 3 CH19                    54 1709.  452. 1323. 1959.
## 4 Capsaicin+ Green tea    54 1649.  450. 1271. 1906.
## 5 placebo                 54 1760.  468. 1302. 1992

group_by will use the column specified to group the data, and the groups are then used when further manipulation is applied to the data frame.

summarise will create a summary of the input data, with the columns specified in the code, calculation the statistics also written in the code (e.g. mn = mean(Totalg) will create a column with the mean of Totalg, for each group in Treatment, as specified by group_by()).

For more information about data manipulation with tidyverse, see Edit using Tidyverse or check out the tidyverse-homepage.

Further, lets print the results in a nice looking table using kable() from the knitr package.

library(knitr)
kable(tb, caption = 'some caption', digits = 0, format = 'simple')

Table 4.1: some caption

Treatment	n	mn	s	q1	q3
Capsaicin	55	1716	473	1314	1943
Green tea	53	1665	462	1213	1912
CH19	54	1709	452	1323	1959
Capsaicin+ Green tea	54	1649	450	1271	1906
placebo	54	1760	468	1302	1992

… and a plot of it:

tb %>% 
  ggplot(data = ., aes(Treatment,mn, ymin = q1, ymax = q3)) + 
  geom_point() + 
  geom_errorbar()

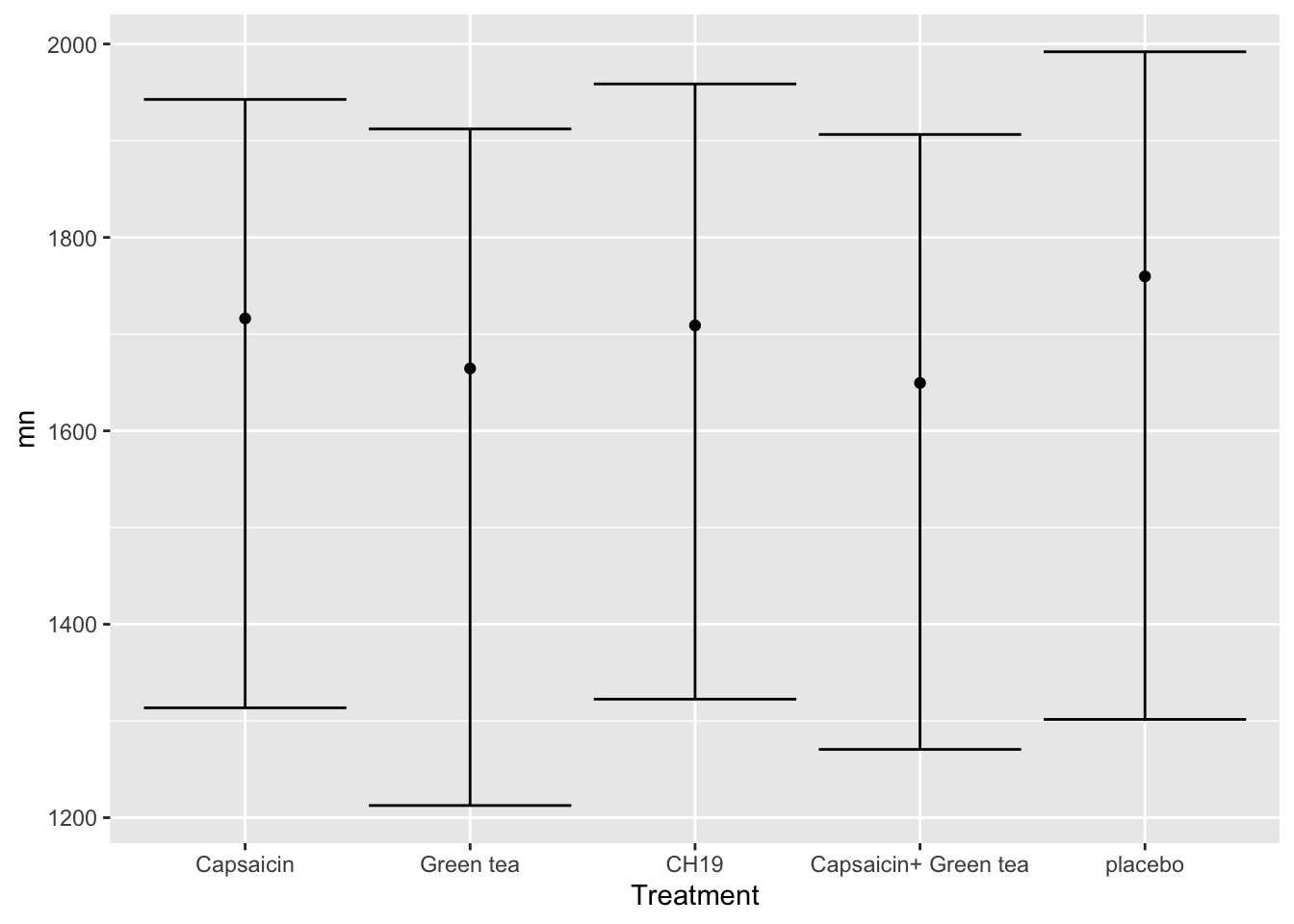
tb %>%: This line is using the pipe operator (%>%), which is native to the dplyr-package and is used in R to chain together multiple operations. It takes the result of the expression on the left and pipes it as the first argument to the function on the right. In this case, tb is being piped into the subsequent operations.

ggplot(data = ., aes(Treatment, mn, ymin = q1, ymax = q3)): This line initiates the creation of a ggplot object using the data from the tb dataset. It specifies the aesthetics (visual mappings) for the plot. Treatment is mapped to the x-axis, mn is mapped to the y-axis, and q1 and q3 are representing the first and third quartile respectively, here graphically represented using errorbars.

geom_point(): This line adds a layer to the plot with points (or dots) representing the data points. Since no aesthetic mappings are provided in this specific line, it’s assumed that the Treatment values are plotted against the mn values on the x- and y-axes.

geom_errorbar(): This line adds another layer to the plot with error bars. The ymin and ymax aesthetics defined in the ggplot() call earlier are used to show the first and third quartile respectively, creating a visual representation of the distribution of the data.

More information on plotting will come in a future chapter (see Plotting data). But try and see if you can make sense of the inputs, and what they correspond to in the plot.